Pregunta 05_2005

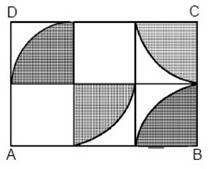
En la figura, ABCD es un rectángulo que se ha dividido en seis cuadrados congruentes . Si los arcos corresponden a cuartos de círculo, entonces ¿cuál(es) de las afirmaciones siguientes es (son) verdadera(s)?

I) La suma de las áreas sombreadas es igual al área de un círculo de radio ..
II) La suma de los perímetros de las áreas sombreadas es igual al perímetro de una circunferencia de radio .
III) La suma de los perímetros de las regiomes sombreadas es  mayor que el perímetro de ABCD.

Alternativas

A)  solo I

B)  solo II

C)  solo III

D)  solo I y II

E)   solo I y III

Curso:  Primero medio

Tema: Congruencia de figuras planas

Comentario

Al analizar la afirmación I), se llega a la conclusión de que es verdadera. En efecto, los cuadrados al ser congruentes tienen todos igual lado y como se tienen cuatro partes iguales de un círculo, iguales entre sí y de radio , entonces la suma de las áreas sombreadas es igual al área de un  círculo con dicho radio.

En la afirmación II), la suma de los perímetros de las 4 áreas sombreadas (con 8 lados rectos en total y 4 semicírculos que forman una circunferencia completa) es ,  y el perímetro de una circunferencia de radio es y como , entonces el perímetro de la circunferencia aludida es , por lo cual resulta falso que tengan igual perímetro.

La afirmación III) es verdadera, porque la suma de los perímetros de las regiones sombreadas es que es mayor que el perímetro del rectángulo ABCD; es decir .

Pregunta fácil, que requiere de conocimientos muy sencillos ( calcular áreas y perímetros en figuras planas), pero que se tornó difícil pues presentó una omisión del 42,3 por ciento y con un tercio de respuestas malas entre quienes la abordaron.

La falla estuvo, creemos, en el análisis de la situación y en la poca aplicación del conocimiento, si es que este último estaba.

Fuente Internet:

Publicación oficial del Demre en www.demre.cl